Es gibt viele Wissenschaftler, die versucht haben, eine Formel zu finden, die sich auch auf alle realen Gase anwenden läßt. Sie haben dabei oft komplizierte Formeln aufgestellt. Hier wird aber nur die von Van-der-Waals gezeigt.

Volumenberichtigung: Wie bei den realen Gasen gesehen, haben die Moleküle ein Eigenvolumen, das bei den idealen Gasen nicht berücksichtigt wird. Van-der-Waals bezeichnete dies mit dem Buchstaben b. Das bezieht sich aber nur auf ein mol. Deswegen muss man b noch mit der Stoffmenge n multiplizieren, um das gesamte Volumen zu erhalten, das die Teilchen einnehmen. Diesen Wert muss man nun von dem gemessenen Volumen abziehen (siehe reale Gase):

(19)

Druckberichtigung: Da bei einem idealen Gas die gegenseitige Anziehung weggelassen wurde, die die Teilchen aufeinander ausüben (siehe: reale Gase), muß man den gemessenen Druck auch noch berichtigen.
Jedes Teilchen im Gas übt eine Anziehung aus, deswegen ist es wichtig, zu wissen, wieviele Teilchen in dem Gas sind. Wir nehmen an, daß das Gas N Teilchen enthält. Die Dichte des Gases ist N/V. Umso größer die Dichte des Gases ist, desto mehr Teilchen stoßen an die Wand. Daraus folgt, daß die Dichte proportional zur Anzahl der stoßenden Teilchen ist. Ebenso ist sie proportional zu den sich zurückziehenden Teilchen. Da es bei größerer Stoffmenge mehr Teilchen sind, ist die Teilchenzahl N der Stoffmenge n proportional. Deswegen kann man N durch n ersetzen. Da es immer zwei Teilchen sind, deren Kräfte aufeinander wirken, muß man quadrieren, und erhält folgendes: (n/V)².
Van-der-Waals nannte den Größenverhältnisfaktor a und erhielt folgende Formel für den Druck, der dazu addiert werden muss:

(20)

Die gesamte korrigierte Formel sieht nun so aus:

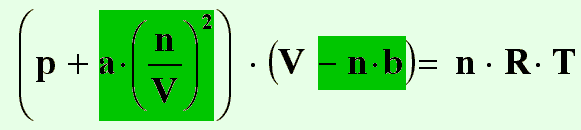
(21)

Die Werte der Konstanten a und b sind für die meisten Gase bereits bestimmt worden. Normalerweise sind die b-Werte von Gasen mit größeren Molekülen größer als Werte der Gase mit kleineren Molekülen. Über die a-Werte kann man sagen, daß Moleküle mit größerer Oberfläche sich gegenseitig stärker anziehen, und deswegen auch größere Werte liefern.
Die Van-der-Waals´sche Gleichung gilt immer noch nicht für alle Druck- und Temperaturbereiche, jedoch ist sie eine bessere Annäherung an das Verhalten von realen Gasen als die ideale Gasgleichung. Bei kleinen Drucken und Zimmertemperatur jedoch kann man sie sehr gut anwenden. Unter diesen Voraussetzungen ist sogar die ideale Gasgleichung relativ genau gültig, sodaß in der Praxis oftmals doch nur mit letzterer gerechnet wird.