Seminar: Generatives maschinelles Lernen: Anwendungen neuronaler Netze bei räumlicher stochastischer Modellierung
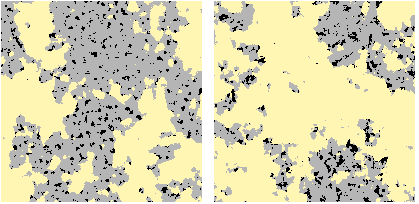
Die quantitative Analyse digitaler (Bild-)Daten ist ein wichtiges Instrument in verschiedenen wissenschaftlichen Disziplinen wie Medizin, Geographie, Wettervorhersage oder Materialwissenschaft. Mathematische Techniken zur Mustererkennung oder zur Beschreibung komplexer Bildstrukturen mit Hilfe von räumlichen stochastischen Modellen können wertvolle Beiträge leisten. Die stochastische Geometrie bietet eine breite Palette an räumlichen stochastischen Modellen für verschiedene Anwendungen, z. B. Punktprozesse zur Beschreibung von Punktmustern im Raum, Zufallsgraphen zur Modellierung komplexer Netzwerkstrukturen und Zufallsmosaike zur Beschreibung von Mosaiken (zellulare oder granulare Strukturen).
Oft erfordern solche Techniken aber explizite Informationen über die Daten, die nur schwer zugänglich sind. In jüngster Zeit haben sich daher Methoden des maschinellen Lernens als nützliches Werkzeug für die Bildverarbeitung und damit auch für die räumliche stochastische Modellierung erwiesen. So können z. B. neuronale Faltungsnetze zur Verbesserung der Bildverarbeitung eingesetzt werden, die oft ein notwendiger Schritt vor der Modellierung ist. Darüber hinaus werden Methoden des maschinellen Lernens zur Vorhersage physikalischer Eigenschaften wie z. B. der Leitfähigkeit von räumlichen stochastischen Modellen verwendet, die ansonsten nur schwer zu berechnen sind. Andererseits können sogenannte generative Netzwerke eingesetzt werden, um direkt neue virtuelle Bilddaten zu erzeugen, welche einem bekannten Datensatz ähnlich sind.
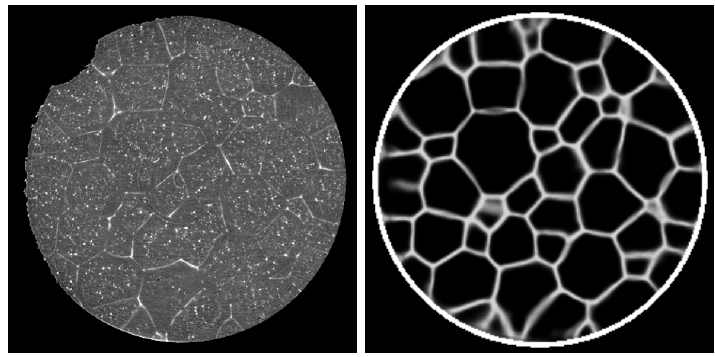
In diesem Seminar werden wir uns daher auf den Einsatz von Techniken des machinellen Lernens in der stochastischen Modellierung fokussieren, wie z.B. Faltungsnetzwerke zur Segmentierung von Bilddaten, generative Netzwerke zum Erzeugen neuer Bilddaten, oder physikalisch informierte Netzwerke zur Vorhersage bestimmter Transporteigenschaften einer Mikrostruktur. Darüber hinaus werden
werden verschiedene wissenschaftliche Studien diskutiert, die die vorgestellten Methoden nutzen. Das Seminar eignet sich als Vorbereitung für die Anfertigung einer Bachelor- oder Masterarbeit zu ähnlichen Themen.
| Voraussetzungen: | Wahrscheinlichkeitsrechnung |
| Zielgruppe: | Bachelor and Master Studenten in "Wirtschaftsmathematik", "Mathematik", "Mathematische Biometrie", "CSE" oder "Lehramt Mathematik" |
| Credits: | 4 |
| Zeit und Ort: | Donnerstags 14:00-16:00; Raum 120, Helmholtzstraße 18. |
| Anmeldung: | per mail an Phillip Gräfensteiner |
Kontakt
Seminar Supervisor
Prof. Dr. Volker Schmidt
E-Mail: volker.schmidt@uni-ulm.de
Dr. Orkun Furat
E-Mail: orkun.furat@uni-ulm.de
Seminar Advisor
Phillip Gräfensteiner
E-Mail: phillip.graefensteiner@uni-ulm.de
Liste der Vorträge:
Using convolutional neural networks for stereological characterization of 3D hetero-aggregates based on synthetic STEM data
| Speaker: | TBD |
| Date: | TBD |
Since 3D imaging is complex and expensive, there are many approaches that attempt to reconstruct the information of a tomographic 3D image from a series of less expensive 2D measurements. In this work, the 3D microstructure of hetero-aggregates is predicted from 2D data. A stochastic model is used to generate synthetic training data on which a convolutional network can be trained [1]. Ultimately, the network can then be used to predict the associated 3D structure from a 2D image.
[1] L. Fuchs, T. Kirstein, C. Mahr, O. Furat, V. Baric, A. Rosenauer, L. Mädler and V. Schmidt, Using convolutional neural networks for stereological characterization of 3D hetero-aggregates based on synthetic STEM data. Machine Learning: Science and Technology 5 (2024), 025007.
Calibration of stochastic geometry models by combining generative adversarial networks with excursion sets of random fields
| Speaker: | TBD |
| Date: | TBD |
Generative adversarial networks (GANs) are a strong data-driven machine learning tool for generating new synthetic image data based on existing data. In order to create a sufficient data base for training these GANs, classical spatial stochastic modeling is deployed in order to generate a virtual data base used for network training. Subsequently, the trained GAN can be used to sample virtual images that can be further analyzed, for example in numerical simulations. This approach has been used to generate virtual data of all-solid-state battery cathodes [2].
[2] O. Furat, J. Schubert, A. Bielefeld, M. Luczak, A. Wiegmann, J. Janek and V. Schmidt, Generative adversarial framework for calibrating an excursion set model for the 3D microstructure of all-solid-state battery cathodes. Working paper (under preparation)
Generative flows for multivariate stochastic modeling
| Speaker: | TBD |
| Date: | TBD |
Real-valued non-volume preserving (NVP) transformations are a class of functions used to construct a general unsupervised learning algorithm for generative probabilistic modeling. Unsupervised learning has the great advantage of not requiring a ground-truth, which is often produced by time consuming hand labelling. The model is trained on four natural image data sets and produces sharp and realistic images, that are qualitatively competitive with other generative probabilistic modeling algorithms [3].
[3] L. Dinh, J. Sohl-Dickstein, and S. Bengio. "Density estimation using real nvp." arXiv preprint arXiv:1605.08803 (2016).
Generative adversarial networks for the generation of multiphase microstructural data
| Speaker: | TBD |
| Date: | TBD |
Generative adversial networks (GANs) which are usually models for unsupervised learning have, for example, various applications in texture and image synthesis [13]. After training with a given data set of images, these networks can generate new images which are statistically similar to those of the training data set. Therefore, GANs can be considered to be spatial stochastic models. For example, in [14] a GAN was trained with with 3D image data depicting the three-phased microstructure of lithium-ion battery cathodes and solid oxide fuell cell anodes. Then, similar to a stochastic geometry model, the trained network is able to generate virtual, but realistic 3D image data.
[13] I.J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, Y. Bengio. Generative adversarial networks (2014). arXiv preprint arXiv:1406.2661.
[14] A. Gayon-Lombardo, L. Mosser, N.P. Brandon, S.J. Cooper. Pores for thought: generative adversarial networks for stochastic reconstruction of 3D multi-phase electrode microstructures with periodic boundaries. npj Computational Materials (2020), 6(1), 1-11.
Generating three-dimensional structures from a two-dimensional slice with generative adversarial network-based dimensionality expansion
| Speaker: | TBD |
| Date: | TBD |
Generative adversarial networks (GANs) can be trained to generate 3D image data based on 3D training data. However, the acquisition 3D image data for model calibration is a time consuming and expensive task. While 2D image data naturally contains much less information, it is possible in some cases that a cross-sectional 2D slice carries enough information to statistically reconstruct the 3D sample. Therefore, a particular GAN-architecture is introduced that is able to generate 3D data based on a single representative 2D image [15].
[15] S. Kench, S.J. Cooper, Generating three-dimensional structures from a two-dimensional slice with generative adversarial network-based dimensionality expansion. Nat Mach Intell 3, 299–305 (2021).