Holomorphe dynamische Systeme und die Riemannsche Vermutung
Die Vorlesung "Holomorphe dynamische Systeme und die Riemannsche Vermutung" hat einen Umfang von 2+1 SWS (4 LP) und ist für Master-Studierende der Studiengänge (Wirtschafts-)Mathematik und CSE.
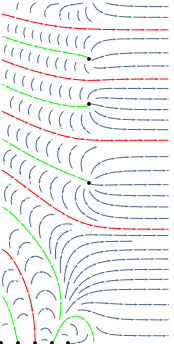
Wir beschäftigen uns in der Vorlesung mit der Riemann'schen Zeta-Funktion und deren Fluss (d.h. die Zeta-Funktion wird zur rechten Seite einer gewöhnlichen Differentialgleichung). Dies ermöglicht einen geometrischen Zugang zur Riemann'schen Vermutung und bietet Verbindungen zur aktuellen Forschung des Dozenten.
Aktuelles
- Die erste Vorlesung findet statt am: voraussichtlich Mi, 18.4.18 (anstelle der Übung)
- Die erste Übung findet statt am: voraussichtlich in der zweiten Semesterwoche
- siehe Moodle (Passwort wird in der ersten Übung oder Vorlesung bekannt gegeben)
Inhalte
In der Vorlesung werden unter Anderem folgende Themen behandelt:
- Die Geschichte der Primzahlen und Zeta-Funktion
- Holomorphe Flüsse und ihre speziellen Eigenschaften
- Das kontinuierliche Newton-Verfahren und Sobolev-Gradienten, Zeta- und Xi-Fluss
- Asymptotik von Flüssen und Phasenraumstrukturen
- Attraktoren und invariante Mannigfaltigkeiten
- Theoretische und numerische Analyseverfahren für dynamische Systeme
Termine
| Vorlesung | Do, 16-18 Uhr | N24, Raum 226 |
| Übungen | Mi, 12-14 Uhr i.d.R. 14-tägig | HeHo 18, Raum E60 |
Literatur
(weiterführende) Literatur:
- H.M. Edwards: Riemann's Zeta Function.
- E.C. Titchmarsh: The Theory of the Riemann Zeta-Function.
- T. Apostol: Introduction to Analytic Number Theory.
- diverse Paper von K. A. Broughan.
