Forschung der Arbeitsgruppe Funken

Um Theorie und Experimente zu ergänzen oder sogar zu ersetzen, müssen die numerischen Simulationen einer Reihe hoher Anforderungen genügen. Das gewählte (mathematische) Ersatzmodell muss die Realität ausreichend genau beschreiben, d.h. die Reaktion des virtuellen System auf Belastungen (Input) spiegelt die Realität möglichst genau wider. Eine wesentliche Forderung an die numerische Mathematik besteht darin, dass die Lösung der Ersatzprobleme in Form z.B. von Randwertproblemen  auf effizientem Weg möglichst genaue und zuverlässige Ergebnisse liefert. Randwertprobleme, wie z.B. die Laplace-, Helmholtz- oder Stokes-Gleichung, lassen sich in ihrem Definitionsbereich  z.B. durch die Finite Elemente Methode (FEM) näherungsweise lösen. 

Überträgt man die Randwertaufgabe in eine Integralgleichung über den Rand des ursprünglichen Gebiets, so lässt sich die gesuchte Lösungsfunktion in einem endlichdimensionalen Unterraum approximieren. Man versucht entweder, die entstehenden Gleichungen in diskreten Knotenpunkten auf dem Rand zur erfüllen (Kollokation), oder durch zusätzliche Integration mit den Basisfunktionen über dem Rand zu lösen (Galerien-Verfahren). Bei der Randelementmethode wird die Dimension des Problems um eins reduziert, was einen wesentlich geringeren Speicherbedarf für die geringere Anzahl der Freiheitsgrade als Unbekannte des zu lösenden Gleichungssystems zur Folge hat. Einerseits sind die Matrizen bei der Boundary Element Methode (BEM) i. allg. voll besetzt, andererseits bietet die Methode bei Außenraumproblemen besondere Vorteile.

Beim numerischen Lösen von PDEs stellt man häufig fest, dass lokale Singularitäten, die z.B.  aus einspringenden Ecken oder Grenzschichten herrühren, nicht gut genug aufgelöst werden. Dies hat zur Folge, dass die Genauigkeit der numerischen Approximation lokal nicht zufriedenstellend ist. Um dieser Problematik Abhilfe zu schaffen, möchte man nahe der kritischen Gebiete feiner diskretisieren. Dafür müssen diese kritischen Gebiete erkannt werden - dafür kommen sogenannte Verfeinerungsindikatoren zum Einsatz. Möchte man den Fehler bestimmen, verwendet man Fehlerschätzer. Zur absoluten Fehlerkontrolle bei der Finite Elemente Methode müssen alle Konstanten in der a-posteriori Fehleranalyse abgeschätzt werden. Mit Lokalisierungsargumenten kann man dies theoretisch wie numerisch durchführen.

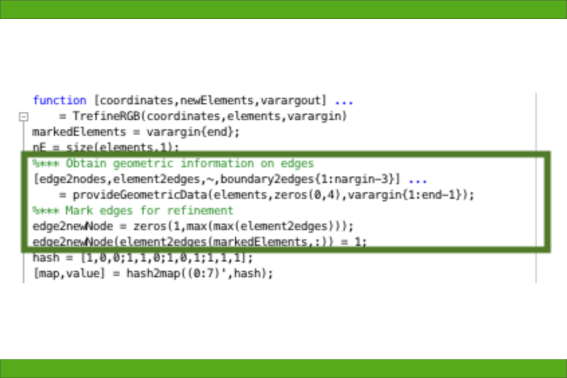
Kommerzielle FEM- und BEM-Programme können in der Regel zwar eine Vielzahl von Problemen lösen, sind aber sogenannte „black boxes“. Diese gewähren dem Nutzer nur sehr eingeschränkten Einblick in die Vorgehensweise. Modifikationen sind i. Allg. nicht möglich, und der Erwerb für Studierende ist recht teuer. Im Gegensatz dazu habe ich mit Kollegen und Studierenden kleine, aber offene und leicht verständliche Matlab-Werkzeuge erstellt, die jeweils auf eine bestimmte Methode zugeschnitten sind. Die Knappheit und Übersichtlichkeit dieser Programme ermöglicht ein gutes Verständnis, den Einsatz in der Lehre und ein leichtes Anpassen an andere Probleme. Studierenden ist es hiermit möglich, viele der numerische Experimente in unseren Numerik-Vorlesungen nachzurechnen, da die Entwicklungzeit solcher Programme häufig deutlich geringer ist als bei üblichen Programmiersprachen (z.B. Fortran, C, C++).

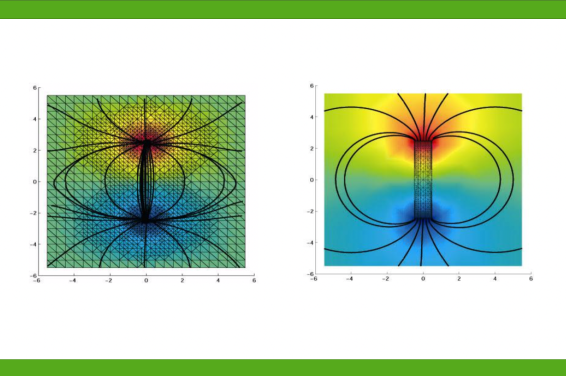
Die beiden wichtigen Verfahren zur Diskretisierung partieller Differentialgleichungen, nämlich Finite Elemente (FEM) und Randelementemethode (BEM), haben komplementäre Eigenschaften. Ihre gewinnbringende Kombination und effiziente Realisierung in Kombination mit hp-Methoden ist eine aktuelle Herausforderung. Exemplarisch sind in den obigen Abbildungen vergleichend Rechnungen für die FEM und FEM-BEM-Kopplung wiedergegeben. Durch „künstliche“ Restriktion von der gesamten Ebene auf ein beschränktes Gebiet ändert sich der Verlauf der Feldlinien deutlich. Es wird somit offensichtlich, daß zur Berücksichtigung eines Außengebiets, die Reduktion auf ein beschränktes Gebiet mit künstlichem Rand nicht genügt und somit die FEM-BEM-Kopplung die Vorteile beider Methoden effizient miteinander verbindet.

Um komplexe Strömungsvorgänge (z.B. Meeresströmungen, Beschichtungsvorgänge) simulieren zu können, müssen adaptive Verfeinerungsstrategien verwendet werden, die die Struktur des räumlichen Finite Elemente Gitters automatisch an die berechenbare Lösung anpassen. Theoretische Grundlage dazu ist effiziente und zuverlässige a-posteriori Fehleranalysis. Anwendungen finden diese Verfeinerungsstrategien z.B. auch in der Simulation der Nasslackierung mit Außenaufladung, welches mit einer adaptive Multilevel FE-BE Kopplung für das elektrostatische Teilproblem in 3 Raumdimensionen gelöst wurde.